# Methodology
The experiment is essentially a series of A/B tests. To test a specific coding construct, we prepare two snippets of code that are identical except in their use of the construct. One snippet will incorporate the coding construct, and the other snippet will incorporate a more neutral alternative.
As an example, one of our tests was to see if expressions that are dependent on operator precedence are more readable with the addition of parentheses. In our experiment we wrote a pair of code snippets as follows:
var fixedCost = 200;
var monthlyCost = 20;
var result = fixedCost + monthlyCost * 12;
var fixedCost = 200;
var monthlyCost = 20;
var result = fixedCost + (monthlyCost * 12);
The two snippets are almost identical, except that the first snippet contains an expression that is dependent on the precedence of the + and * operators, while the second removes the ambiguity by adding parentheses.
The idea is to observe the behaviour of developers as they read the snippets and compare the readability of the two constructs.
# Metrics for readability
Rather than asking a developer whether they find the code readable, the experiment attempts to objectively measure the readability of the snippets by directly observing the behaviour of the developer reading them. Specifically, we measure two factors:
- Accuracy: Can the developer predict the output of the code snippet correctly. This gives us a metric for whether or not they have understood the code.
- Time taken: If they correctly predicted the code's output, how long did they spend reading the code to get to that understanding.
We define readability as the combination of these two metrics. The quicker a developer can come to a correct understanding of what the code does, the more readable we consider the code.
# Procedure
The process for a participating developer was as follows:
The developer agrees to take part in the experiment and provides information on how long they have been programming and the main language they work in.
They are presented with instructions for the experiment and tips on how to take part.
They are then presented with a code snippet and a timer is started in the background.
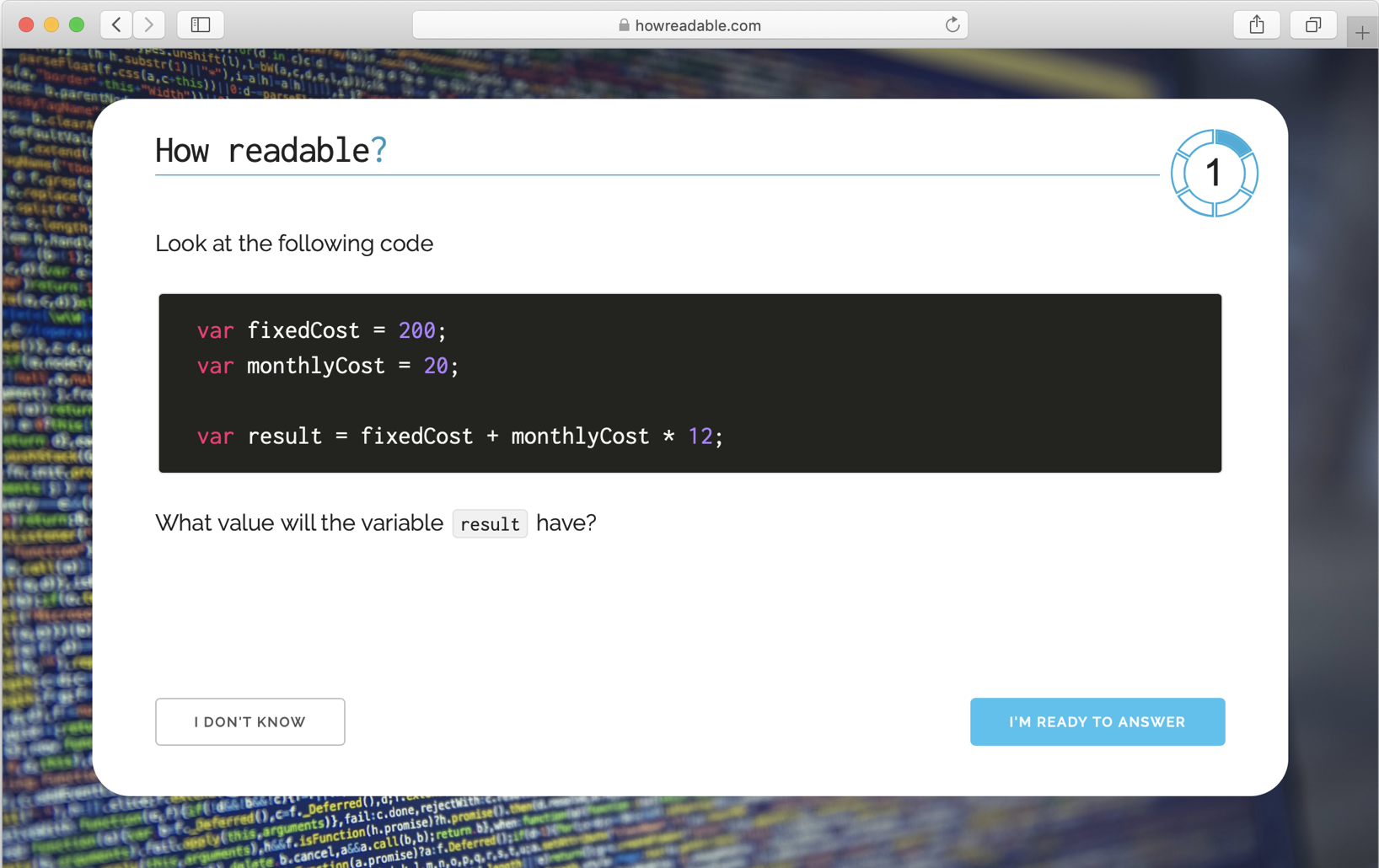
The developer is asked to read the code snippet and to answer a question about it. The snippets all contain a variable named
result, and the participant is asked to predict what the value of the variable would be after the code was run.When the developer feels they are ready to answer, they click a button, and the timer is stopped. The code is then replaced by multiple-choice options for the value of the variable result. There is also an option for "I don't know".
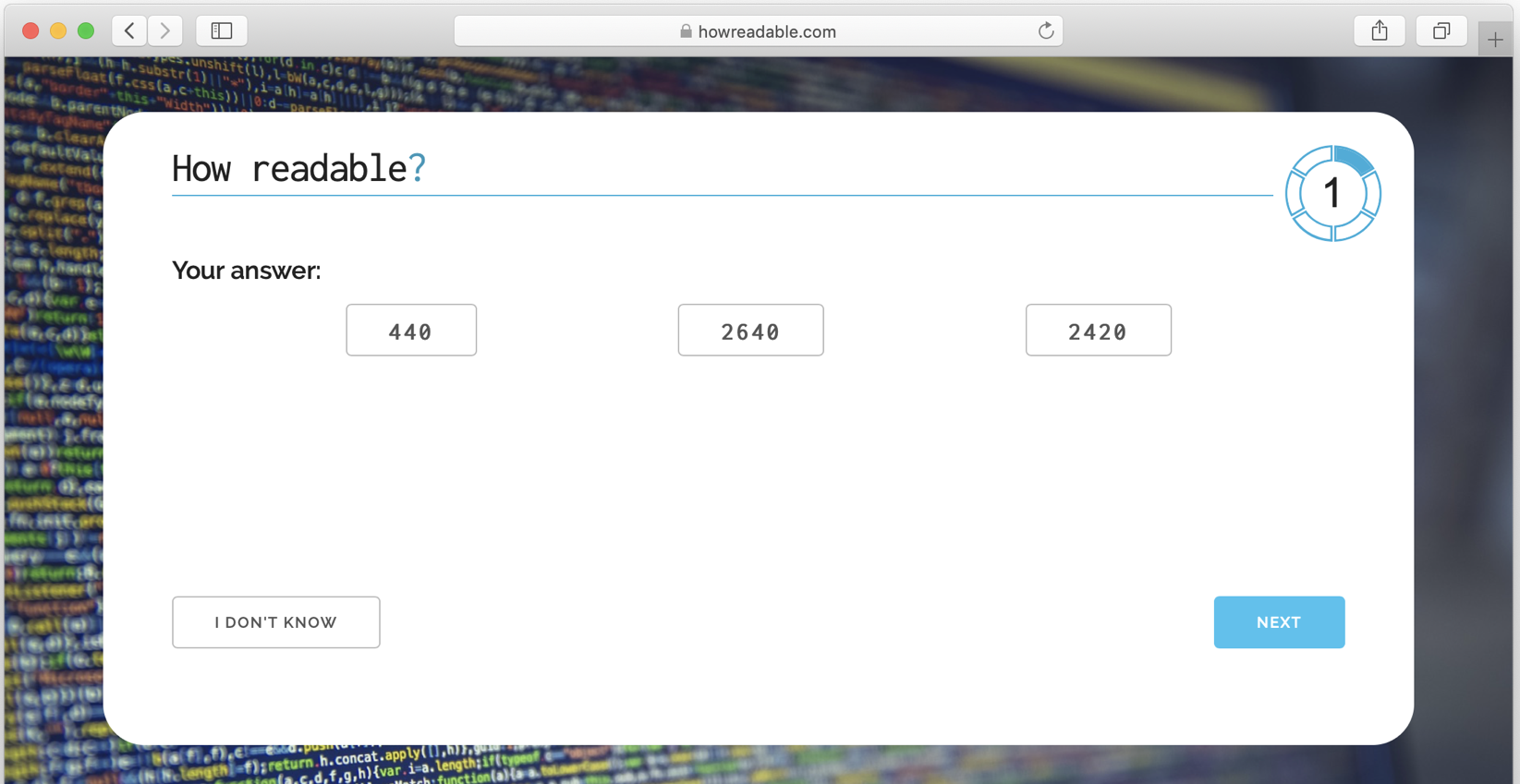
After selecting an option, we record the time taken reading the code and the selected option.
Steps 3 - 6 are then repeated with further code snippets, for as long as the developer is willing to continue.
There are two output metrics; the amount of time taken viewing the snippet, and whether the selected answer was correct.
# Exercises
In total there were 11 experiments, with each measuring a different coding construct. For each experiment, we wrote a series of six coding exercises. An exercise consisted of a pair of code snippets that were identical apart from the construct being measured.
The snippets were written in JavaScript using ES5 syntax. We wanted as many programmers as possible to participate in the experiment and it was felt that ES5 was the most widely understood language available.
You can see the source code for the exercises that produced results here.
The snippets were designed so that:
- They were short enough to be read without excessive scrolling.
- They were self-contained and did not rely on any external variables or modules.
- Any calculations involved could easily be done mentally.
- There was a unique, well-defined value for the resulting variable
A participating developer would start one of the experiments, chosen at random, and be asked to complete all six exercises. The exercises were presented in a random order, and for each exercise, the participant was shown one of the two snippets at random.
After completing an experiment, the developer was asked whether they would be willing to start another. On average the participants completed two experiments.
The hope was that by showing the participant six separate exercises involving the same construct, we could mitigate any delay in reading the code caused by unfamiliarity with the experimental process.
# Statistical Analysis
For each experiment, we calculated two output metrics for the two coding constructs.
- The percentage of participants that correctly predicted the value of the output variable
- The average time spent reading the code by participants who correctly predicted the output.
Note that we were only interested in the time taken reading the code if the participant correctly predicted the resulting variable. The time taken to not understand the code does not tell us anything useful.
We aggregated these two metrics across all six exercises. Any inherent difference in time taken or accuracy between exercises, would not affect the averages as the effect should be the same for both snippets of a particular exercise. Any difference in the aggregated averages should be attributable to the use of the constructs themselves.
We did not correlate the results of an individual participant. The results of the six exercises seen by a single participant were treated as six separate data points.
There was no way to ensure that while the participant had the code page open, they spent all the time reading the code. As a result, we considered it reasonable to remove any outliers from the measurements for the time taken. Outliers were identified using the standard method of Tukey Outer Fences
To calculate the statistical significance of differences in the time taken to read the code, we used a two-tailed Welch's t-test. Tests were run to verify that the calculated means were normally distributed and that a t-test would therefore apply.
To calculate the statistical significance of the difference in accuracies, a Chi-squared test was used. There were two categories for each pair of constructs; the number answering correctly and number answering incorrectly.
We are very grateful to Oskar Holm for his help with the statistical analysis.
← Introduction Results →